Hukum Newton
[sunting]Hukum I Newton
Setiap benda akan tetap diam atau bergerak lurus beraturan apabila pada benda itu tidak bekerja gaya.

[sunting]Hukum II Newton
Bila sebuah benda mengalami gaya sebesar F maka benda tersebut akan mengalami percepatan.

Keterangan:
- F : gaya (N atau dn)
- m : massa (kg atau g)
- a : percepatan (m/s2 atau cm/s2)
[sunting]Hukum III Newton
Untuk setiap gaya aksi, akan selalu terdapat gaya reaksi yang sama besar dan berlawanan arah.

[sunting]Gaya gesek

Keterangan:
- Fg : Gaya gesek (N)
 : koefisien gesekan
: koefisien gesekan- N : gaya normal (N)
[sunting]Gaya berat

Keterangan:
- W : Gaya berat (N)
- m : massa benda (kg)
- g : gravitasi bumi (m/s2)
[sunting]Berat jenis
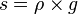 atau
atau 
Keterangan:
- s: berat jenis (N/m3)
- w: berat benda (N)
- V: Volume benda (m3)
 : massa jenis (kg/m3)
: massa jenis (kg/m3)
[sunting]Tekanan

Keterangan:
- p: Tekanan (N/m² atau dn/cm²)
- F: Gaya (N atau dn)
- A: Luas alas/penampang (m² atau cm²)
Satuan:
- 1 Pa = 1 N/m² = 10-5 bar = 0,99 x 10-5 atm = 0,752 x 10-2 mmHg atau torr = 0,145 x 10-3 lb/in² (psi)
- 1 torr= 1 mmHg
[sunting]Tekanan hidrostatis


Keterangan:
- ph: Tekanan hidrostatis (N/m² atau dn/cm²)
- h: jarak ke permukaan zat cair (m atau cm)
- s: berat jenis zat cair (N/m³ atau dn/cm³)
- ρ: massa jenis zat cair (kg/m³ atau g/cm³)
- g: gravitasi (m/s² atau cm/s²)
[sunting]Hukum Pascal
Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah.

Keterangan:
- F1: Gaya tekan pada pengisap 1
- F2: Gaya tekan pada pengisap 2
- A1: Luas penampang pada pengisap 1
- A2: Luas penampang pada pengisap 2
[sunting]Hukum Boyle
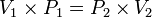
Hukum Pertama Termodinamika
Perubahan energi dalam: 

Keterangan:
 :Perubahan energi dalam (Joule)
:Perubahan energi dalam (Joule)- U2:Energi dalam pada keadaan akhir (Joule)
- U1:Energi dalam pada keadaan awal (Joule)
Usaha yang dilakukan oleh gas pada tekanan tetap:
Keterangan:
- p: Besarnya tekanan (atm)
 : Perubahan volume (liter)
: Perubahan volume (liter)
Rumus umum usaha yang dilakukan gas: 

Penghitungan energi dalam:
- Gas monoatomik:

- Gas diatomik:

[sunting]Proses-proses termodinamika gas
[sunting]Proses isobarik
Proses isobarik adalah perubahan keadaan gas pada tekanan tetap.
Persamaan keadaan isobarik: 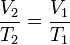
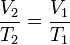
Usaha yang dilakukan pada keadaan isobarik: 

[sunting]Proses isokhorik
Proses isokhorik adalah perubahan keadaan gas pada volume tetap.
Persamaan keadaan isokhorik: 

[sunting]Proses isotermis/isotermik
Proses isotermik adalah perubahan keadaan gas pada suhu tetap.
Persamaan keadaan isotermik: 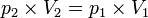
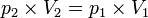
Usaha yang dilakukan pada keadaan isotermik:
- Dari persamaan gas ideal

- Rumus umum usaha yang dilakukan gas:

maka: 

karena 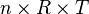 bernilai tetap, maka:
bernilai tetap, maka:
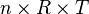 bernilai tetap, maka:
bernilai tetap, maka:
Ingat integral ini!


maka persamaan di atas menjadi
maka menjadi:
[sunting]Proses adiabatik
Proses adiabatik adalah perubahan keadaan gas dimana tidak ada kalor yang masuk maupun keluar dari sistem.
Persamaan keadaan adiabatik: 

Tetapan Laplace: 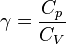
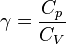
karena  , maka persamaan diatas dapat juga ditulis:
, maka persamaan diatas dapat juga ditulis:
 , maka persamaan diatas dapat juga ditulis:
, maka persamaan diatas dapat juga ditulis:
Usaha yang dilakukan pada proses adiabatik: 







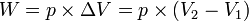



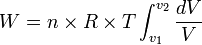
![W = n \times R \times T \times[\ln V_2 - \ln V_1]](http://upload.wikimedia.org/math/0/a/7/0a71834fa480baf975b62a9a64bb7b7d.png)


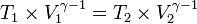

0 komentar:
Posting Komentar